논문: SimGNN: A Neural Network Approach to Fast Graph Similarity Computation

❍ WSDM 2019
❍ network embedding, neural networks, graph similarity computation, graph edit distance
ABSTRACT
그래프 유사도 검색 > 그래프 편집거리(GED), 최대 공통 부분 그래프(MCS)
그래프 문제를 해결하기 위한 새로운 신경망 기반 접근법 제안
1. 학습 가능한 임베딩 함수 설계
- 그래프를 임베딩 벡터로 매핑: 그래프의 요약 정보 제공
- 새로운 attention 메커니즘 도입: 유사도 지표에 따라 중요 노드 강조
2. pairwise node comparison: supplement the graph-level embeddings with fine-grained nodelevel information
1. INTRODUCTION
사용자 쿼리가 주어졌을 때, DB에서 유사한 그래프 집합 검색
- 유사도: GED, MCS 를 지표로 사용 -> 계산 작업은 NP-Complete문제로 알려져 있다.
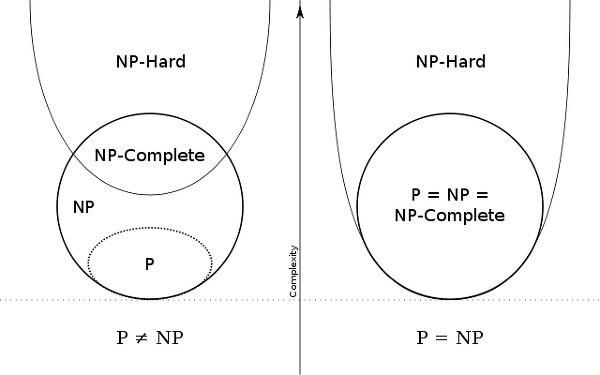
P Problem
: Polybnomial Time 안에 해결할 수 있는 문제, 문제에 대해 동일한 해답을 주는 알고리즘 있을 때 해당 문제는 해결 가능
NP Problem
:Non-determinstic Polynomial Tme Probelm, 다항식 시간 내에 해결할 수 있는지 없는지 모르는 문제
(P ⊆ NP라고 할 수 있지만 NP ⊆ P인지는 알 수 없음)
NP-Hard Problem
"모든 NP 문제를 다항식 시간 내에 'A' 문제로 reduce/transform 할 수 있는 경우 'A' 문제를 NP-hard라고 한다."
=> NP에 속하는 모든 문제에 대해, 다른 문제로 polynomial-time many-one reducible 되는 문제
NP-Complete Problem
NP-Hard 이면서 NP 에 속하는 문제
❍ 그래프 유사도 검색 방안
1. Pruning-Verification framework
쿼리에 대한 정확한 그래프 유사도 계산의 총 양을 데이터베이스 인덱싱 기법과 프루닝을 이용해 줄여
-> 그래프 유사성 계산의 시간 복잡도는 해결 못해
2. Reduce the cost of graph similarity computation
- 정확한 similarity metirc을 계산하는 대신, approximate value를 빠르고 heuristic 한 방법으로 찾아
-> 복잡한 설계/구현 필요
-> 시간 복잡도 여전히 polynomial or sub-exponential (A*-Beamsearch)
=====
논문에서는 속도를 높일 수 있는 새로운 접근법 제안
Reduce the cost of graph similarity computation => approximate similarities를 직접 계산하는 대신,
combinatorial search 사용 -> Learning problem
= 한 쌍의 그래프를 유사성 점수로 매핑하는 신경망 기반 함수 설계
[Training Stage]
predicted similarity scores <-> ground truth 차이 최소화
- training data: pair of graphs together with their true similarity score
[Test Stage]
학습된 함수에 임의의 그래프 쌍 제공, 유사성 점수 예측
-> SimGNN: Similarity Computation via Graph Neural Networks
❍ SimGNN 설계
(1) Representation-invariant: 동일한 그래프를 노드의 순서를 바꾸면 서로 다른 인접 행렬로 나타낼 수 있다 => 계산된 유사성 점수는 이런 변화에 불변해야 함
(2) Inductive: should generalize to unseen graph
(3) Learnable: 모델은 학습을 통해 매개변수를 조정, 어떤 similarity metric에도 적응해야 한다.
=> 학습 가능한 임베딩 함수 설계, 각각의 그래프 > 임베딩 벡터로 변환: 노드 수준의 임베딩 종합해 그래프 전체를 요약
=> 특정 유사도 지표에 따라 전체 그래프에서 중요한 노드 선택하기 위한 새로운 어텐션 메커니즘

그래프 A는 임베딩 공간에서 Q와 가까워, 실제 유사성: A와 Q 비슷
* 임베딩 기반의 유사도 계산은 매우 빠르다
* 그래프 수준의 임베딩 -> 노드 수준 보완 : pairsiwe node comparision method
하나의 고정 길이 임베딩은 그래프 단위로 불완전 < 두 그래프의 노드 쌍별 유사도 점수 계산
=> 유사도 점수로부터 히스토그램 추출, 그래프 수준 정보와 결합
? 히스토그램의 사용 이유 ?
1. 정보 요약: 노드 쌍 별 유사도 점수 분포를 그대로 사용 X, 히스토그램으로 나타내면 데이터 특성을 한눈에 파악 가능
2. 차원축소: 노드 쌍별 유사도 직접 사용보다 히스토그램 사용 시, 데이터 차원 줄일 수 있다.
❍ CONTRIBUTION
- 그래프 유사도 계산이라는 문제를 학습 문제로 고려, 이를 해결하기 위한 SimGNN 이라는 신경망 기반 접근 방식 제안
- 효율적/효과적인 어텐션 메커니즘 제안 -> 그래프 간 유사성 보존하는 그래프 레벨의 임베딩 만들어내는데 필요
- pairwise 노드 비교 방법 사용 -> 그래프 수준 임베딩 보완 : 그래프 간 유사성 보존하는 효과적인 임베딩 얻어
- 실제 네트워크 데이터셋 기반으로 실험 진행
2. PRELIMINARIES
2.1 Graph Edit Distance (GED)

G1과 G2 간의 GED: G1 -> G2로 변환하는 과정에서 수행되는 edit operation 의 수
* edit operatrion: vertex/edge 의 삽입, 삭제, relabelling
* 그래프가 동일하다면 둘의 GED = 0
그래프 간의 거리가 계산된 후 0~1 사이의 유사도 점수로 변환 (* 변환 방법은 4.2)
2.2 Graph Convolutional Networks (GCN)
📌 GCN
Convolution Filter(kernel)로 imgage 순회, dot-product, 기존의 데이터로부터 filter 이용해
새로운 tensor(=activation map) 만들어
filter의 depth = receptive field, 깊을수록 더 깊은 computation layer
conv 연산의 특징 - weight sharing
node feature matrix update
graph 주변의 부분들로 update
> conv 연산과 비슷하게 local 정보 이용하고 weight sharing
Node embedding computation
[1] compute graph-level embedding
[2] pairwise node comparison for 2 graph
노드 임베딩 알고리즘 중, Graph Convolution Network, GCN 사용 <- 다른 임베딩 알고리즘???
- initialization is carefully designed.
- inductive, since for any unseen graph


N(n): set of the first-order neighbors of node n, n itself
dn: degree of node n + 1
W: weight matrix associated with eht l-th GCN layer
b: bias
f: activation fuction (ReLU)
3. THE PROPOSED APPROACH: SIMGNN
한 쌍의 그래프를 유사성 점수로 매핑하는 학습: end-to-end neural network
** end-to-end neural network
입력 ~ 출력 까지 전체 과정을 하나의 통합된 신경망으로 처리하는 기술
입력-출력 사이의 매핑을 자동으로 학습 가능, 중간 단계의 특징 추출과 전처리 과정의 번거로움 줄여준다
3.1 Strategy One: Graph-Level Embedding Interaction
그래프 수준 임베딩이 그래프의 구조/특징 정보를 인코딩할 수 있고
이를 통해 두 그래프간의 유사성을 예측할 수 있다는 가정 기반
(1) node embedding stage: 그래프 노드 -> 벡터 임베딩
(2) graph embedding stage: 각 그래프에 대해 하나의 임베딩 생성 (by attention based aggregation)
(3) graph-graph interaction stage: 두 그래프 임베딩으로부터 유사성 점수 반환
(4) final graph similarity score computation stage: 앞 단계의 유사성 점수 -> 하나의 최종 점수로

3.1.1 Stage 1 - Node Embedding
GCN 사용 (Neighbor aggregation based method) 🚩 GCN

invariant를 표현하는 aggregation func을 학습하고 unseen node에 적용할 수 있다.
=> node embedding 후 attention module에 넣을 준비 완료!
3.1.2 Stage II: Graph Embedding
노드 임베딩 집합을 이용해 각 그래프마다 하나의 임베딩을 만들기 위해서?
* unweighted average of node embeddings
* weighted sum where a weight associated with a node is determined by its degree.
=> specific similarity metric에 따라 어떤 노드는 더 중요해 높은 가중치를 두어야 할 것
본 논문에서 다음과 같은 어텐션 메커니즘 제안

* nodes similar to the global context should receive higher attention weights
시그모이드 함수 사용해 attention weight 0~1 사이의 값으로 조절
<-> 길이를 1로 정규화 하지 않는다. 임베딩 norm 이 그래프 사이즈를 반영하도록 두는 것이 바람직. 그래프 유사도 계산에 필수적 작업!!

3.1.3 Stage III: Graph-Graph Interaction: Neural Tensor Network.
단순 내적을 통해 계산할 수 있지만, lead to insufficient or weak interaction between the two의 가능성
본 눈문에서는 Neural Tensor Networks (NTN)🚩 to model the relation between two graph-level embeddings 사용
3.1.4 Stage IV: Graph Similarity Score Computation.
list of similarity scores를 얻으면, standard multi-layer fully connected neural network를 적용해 similarity score vector의 차원을 점차 줄인다.

compared against the ground-truth similarity score using the following mean squared error loss function:
3.1.5 Limitations of Strategy One.
그래프 레벨 임베딩에서 노드 레벨 정보(노드 특징 분포, 그래프 사이즈)가 손실될 수 있다.
=> 단어 수준의 정보를 사용하면 ? 자연어 처리에서 문장 당 하나의 임베딩 기반으로 한 매칭의 성능 향상 가능
3.2 Strategy Two: Pairwise Node Comparison

주어진 2개의 그래프 크기가 달라 two fake nodes with zero embedding are padded to the graph
+ 그래프 표현의 불변성을 보장하기 위해 노드에 순서를 지정하는 방법을 적용해 전처리 할 수 있지만
-> 히스토그램 사용
: 연속적이지 않고, 미분 가능하지 않아 : 역전파를 통한 모델 훈련에 직접 사용 불가능
=> [strategy 1]로 모델 가중치 업데이트, 그래프 수준 임베딩 생성, 그래프 간의 구조적, 특성 유사성 반영에 효과적
=> [strategy 2]로 그래프 특징 보완해 성능 향상, 노드 간의 세부적 유사성 이해, 역전파 지원 X (유사도 계산에만 사용), 모델 훈련에 직접 기여 X
3.3 Time Complexity Analysis
SimGNN이 훈련되면, 어떤 그래프에 대해서 유사도 점수 계산하는데 사용 가능
* The node-level and global-level embedding computation stages.
임베딩 계산 단계는 각 그래프마다 한번씩 계산
generation of node-level and graph-level embedding : O(E) (E: number of edges)
graph-level 임베딩은 pre-computed 되어 저장.
setting of 그래프 유사도 검색에서, unseen query graph는 그래프 임베딩을 얻기 위해 한 번만 처리하면 된다.
* The similarity score computation stage.
모든 그래프 쌍에 대해 계산

4 EXPERIMENTS
4.1 Datasets

4.2 Data Preprocessing
* AIDS and LINUX are relatively small, an exponentialtime exact GED computation algorithm named A *🚩
“no currently available algorithm manages to reliably compute GED within reasonable time between graphs with more than 16 nodes.”
IMDB 데이터셋 처리-> Beam, Hungarian, VJ 🚩 같은 근사 알고리즘 사용
최소값을 선택하는 이유? 근사 알고리즘이 반환하는 GED가 실제보다 크거나 같다는 것이 보장되기 때문!
실제 GED와 오차를 최소화 하면서 정확한 값을 얻을 수 있다.

4.3 Baseline Methods
(1) fast approximate GED computation algorithm
- A*
- Hungarian
- VJ
(2) neural network based
- SimpleMean simply takes the unweighted average of all the node embeddings of a graph to generate its graph-level embedding.
- HierarchicalMean
- HierarchicalMax are the original GCN architectures based on graph coarsening, which use the global mean or max pooling to generate a graph hierarchy.
(The next four models apply the attention mechanism on nodes.)
- AttDegree uses the natural log of the degree of a node as its attention weight
- AttGlobalContext
- AttLearnableGlobalContext (AttLearnableGC) both utilize the global graph context to compute the attention weights, but the former does not apply the nonlinear transformation with learnable weights on the context, while the latter does.
- SimGNN is our full modek that graph combines the best of Strategy 1 (AttLearnableGC) and Strategy 2.
4.4 Parameter Settings
- the number of GCN layers = 3
- activation function = ReLU
[training]
- batch size = 128
- Adam algorithm for optimization
- learning rate = 0.001
- number of iterations = 10000
- select the best model on the lowest validation loss
4.5 Evaluation Metrics
- Time
- Mean Squared Error
- Spearman’s Rank Correlation Coefficient (ρ)
- Kendall’s Rank Correlation Coefficie (𝛕)
> Precision at k (p@k). p@k is computed by taking the intersection of the predicted top k results and the ground-truth top k results divided by k. Compared with p@k, ρ and τ evaluates the global ranking results instead of focusing on the top k results.
4.6 Results
4.7 Parameter Sensitivity
4.8 Case Studies
5. RELATED WORK
5.1 Network/Graph Embedding
- node-level embedding
- graph-level embedding
- graph neural network applications
5.2 Graph Similarity Computation
- graph distance/similarity metrics
- Pairwise GED computation algorithms
- Graph Similarity search
6. DISCUSSIONS AND FUTURE DIRECTIONS
- edge 특성은 처리할 수 없다
- precision 을 향상시키기 위해 top k 개의 결과에서 다른 기법을 탐색 -> 훈련 데이터셋의 유사도 분포가 비대칭적
- 큰 그래프에 대해 정확한 GED 계산할 수 없다는 제약 -> 작은 그래프 사이의 정확한 GED 만으로 훈련된 모델이 큰 그래프에 대해 어떻게 일반화 되는가?
7. CONCLUSION
"The central idea is to learn a neural network based function that is representation-invariant, inductive, and adaptive to the specific similarity metric, which takes any two graphs as input and outputs their similarity score."
📌 [07.18] SEMINAR FEEDBACK
- 후보 집합 빠르게 찾아내기
- 두 그래프 사이의 노드 - 매칭 sequence 찾기
<= Ptr-Net과 엮어, Graph-level embedding interatcion 적용 ??
* Pairwise Node Comparison
: 히스토그램의 역할? 왜 ? 어떻게?
그래프 유사성 검색
- (GED) Graph Edit Distance
- (MCS) Maximum Common Subgraph
노드/그래프 분류 등 응용 프로그램에 대한 신경망 접근 방식
> 좋은 성능 유지하면서 계산 부담 완화하기
SimGNN의 전략
(== GED 계산에 대해 근사 알고리즘 및 신경망 모델 비교했을 때 좋은 성능)
1. 모든 그래프를 임베딩 벡터에 매핑하는 학습 가능한 임베딩 함수 설계 > 전체 그래프에 대한 정보 제공
++ 특정 유사성 메트릭과 관련한 중요한 노드를 강조하기 위해 어텐션 메커니즘 사용
2. 노드 수준 정보를 사용해 그래프 수준 임베딩을 보완 > pairwise comparison
++ 두 그래프 노드 쌍별 유사도 점수 계산 > 히스토그램 추출 > 그래프 level 정보와 결합
>>> Representation Invariant
동일한 그래프는 노드 순서 바꾸면 다른 인접 행렬로 표현 -> 유사도 점수는 이런 변화에 대해 불변
>>> Inductive
should generalize to unseen graph.
>>> Learnable
학습을 통해 유사도 지표에 적응할 수 있어, 모델 파라미터 조정해 다양한 유사도 지표에 대응
(GCN) Graph Convolutional Networks
- node embedding 방법
- 초기화 잘 하면 representation Invariant
- unseen graph 에 대해서도 ㅇㅇ
A* 알고리즘: 최단 경로 탐색
시작 노드만 지정, 다른 모든 노드에 대한 최단 경로 파악하는 다익스트라와 다르게
시작 - 목적지 노드를 분명하게 지정해, 두 노드간의 최단 경로 파악
휴리스틱 추정값을 통해 개선 가능
'👩💻 도비는 공부중 > 📋 연구과제(2023.7 ~ )' 카테고리의 다른 글
| [용어정리] 쫌쫌따리 정리하는 개념들 (0) | 2023.07.30 |
|---|---|
| [Setup] Window | Anaconda | Pytorch | CUDA | CUDNN (0) | 2023.07.21 |
| NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE (0) | 2023.07.19 |
| [세미나] 준비 과정 | 시작이 절반 | 발표는 어려워 | 피드백 (1) | 2023.07.19 |
| Set-to-Sequence Methods in Machine Learning:a Review (0) | 2023.07.14 |


